正三棱锥各个面相等吗 画出正三棱锥的三视图

正三棱锥是一种由一个正三角形底面和三个全等三角形侧面的三维多面体。正三棱锥的各面相等，具有对称性。

侧面积

正三棱锥的侧面积等于三个全等三角形面积的总和。由于侧面的底边相等，高度相等，因此每个三角形的面积相等。令侧面的底边为 \(a\)，高度为 \(h\)，则侧面积为：

侧面积 = 3 × (1/2) × a × h = 3/2 × a × h

底面积

正三棱锥的底面是一个正三角形，其面积等于三角形面积公式：

底面积 = (1/4) × √3 × s^2

其中 \(s\) 是三角形的边长。

表面积

正三棱锥的表面积等于侧面积和底面积之和。根据上述公式，正三棱锥的表面积为：

表面积 = 侧面积 底面积

= 3/2 × a × h (1/4) × √3 × s^2

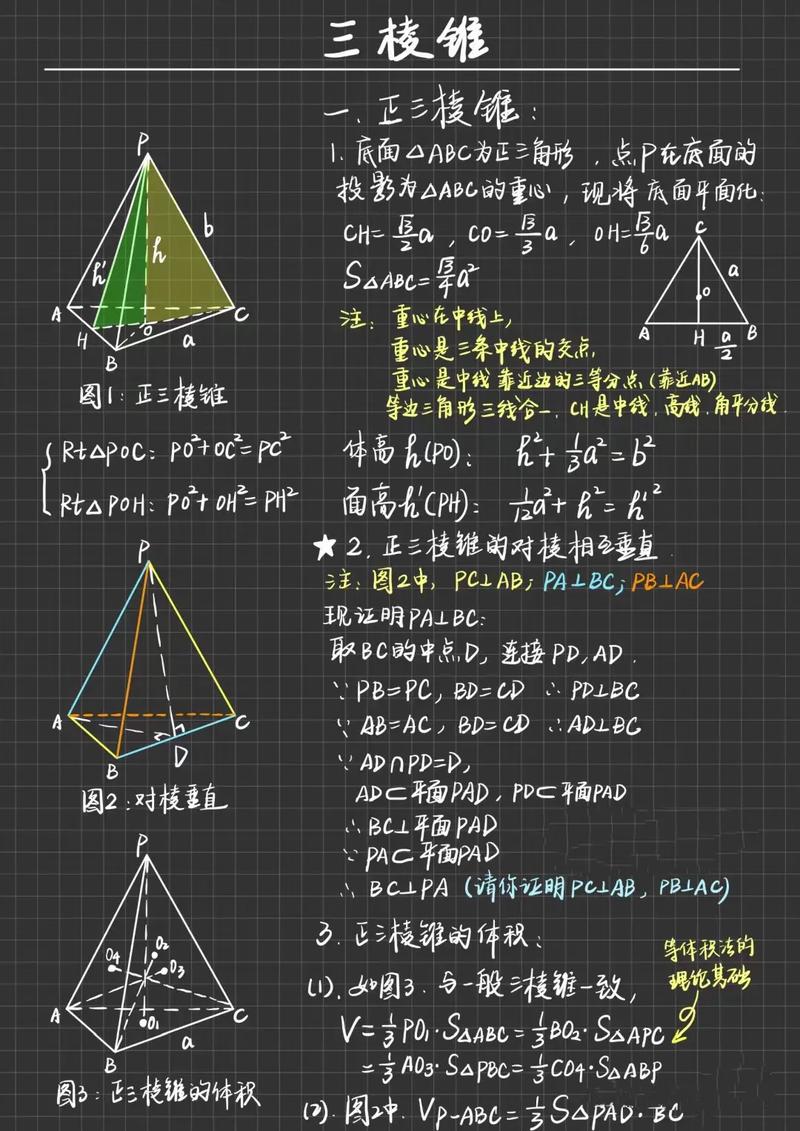
正三棱锥有何特点

体积

正三棱锥的体积等于底面积乘以底面到顶点的垂高再除以 3。令底面积为 \(B\)，垂高为 \(H\)，则体积为：

体积 = (1/3) × B × H

对称性

正三棱锥具有对称性。它沿中心对称轴旋转 120° 或 240°，都能与自身重合。

示例

如果正三棱锥的侧面的底边长为 5 厘米，侧面的高度为 8 厘米，底面的边长为 6 厘米，则：

侧面积 = 3/2 × 5 × 8 = 60 平方厘米

底面积 = (1/4) × √3 × 6^2 = 9√3 平方厘米

表面积 = 60 9√3 平方厘米

体积 = (1/3) × 9√3 × 8 = 24√3 立方厘米

正三棱锥的各个面相等，这意味着它的侧面积、底面积和表面积等。正三棱锥具有对称性，旋转 120° 或 240° 与自身重合。