三个平面相交形成的角 形成二个角的图形

在几何的浩瀚宇宙中，三平面相交形成的角像是一道神秘的光芒，照亮了我们对空间的理解。这些角度不仅构成了空间中的基本元素，还揭示了几何学中最复杂的关系。本文将深入探讨三平面相交角的几何特性、计算方法及其在实际应用中的重要性，带你进入这个令人着迷的数学领域。

三平面相交角的基础概念

我们必须明确“三平面相交”这一概念。简单来说，三平面相交意味着三个平面在空间中相交，形成一个复杂的交点和角度组合。每个交点处，都存在一个由这三个平面相互交织所形成的角。了解这些角的特性对于进一步研究空间几何至关重要。

计算三平面相交角的方法

要准确计算三平面相交角，我们可以使用向量代数和空间解析几何的方法。设平面方程为

A_1x B_1y C_1z D_1 = 0

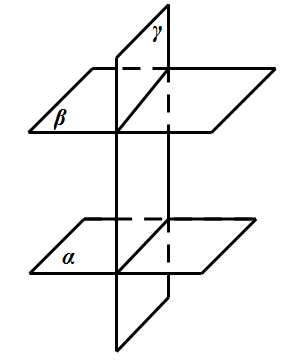
两个平面相交的交线平行于平面吗

A_2x B_2y C_2z D_2 = 0

A_3x B_3y C_3z D_3 = 0

。计算每两个平面的法向量之间的夹角，然后通过这些夹角确定三平面相交处形成的角。这一过程需要的数学推导，最终得到的结果将揭示出角度的值。

实际应用中的重要性

理解和计算三平面相交角在多个领域具有实际意义。在建筑设计中，工程师需要地计算结构交点的角度，以确保建筑的稳定性。在计算机图形学中，三维建模中的角度计算帮助创建逼真的视觉效果。在机械工程和机器人领域，三平面相交角的计算对于设计精密的机械部件至关重要。

三平面相交角不仅是几何学中的基础概念，它的深入研究还能够揭示空间中的复杂关系。通过的计算和分析，我们能够在多个实际应用领域中发挥其重要作用。探索这些角度的奥秘，不仅能够提升我们对空间几何的理解，还能在实际问题中提供有效的解决方案。无论你是几何学爱好者还是专业研究者，三平面相交角的研究都将带给你无穷的启发和挑战。